CPU Testing Methodology Part 2

In Part 1 we addressed how to take and process good data for a single data run on a CPU block.  Now we’re going to look at multiple mounts.  In previous roundups I’ve done 5 or 6 mounts of a block.  Generally I’ve averaged all the data, although sometimes I’ve experimented with excluding the worst data point.

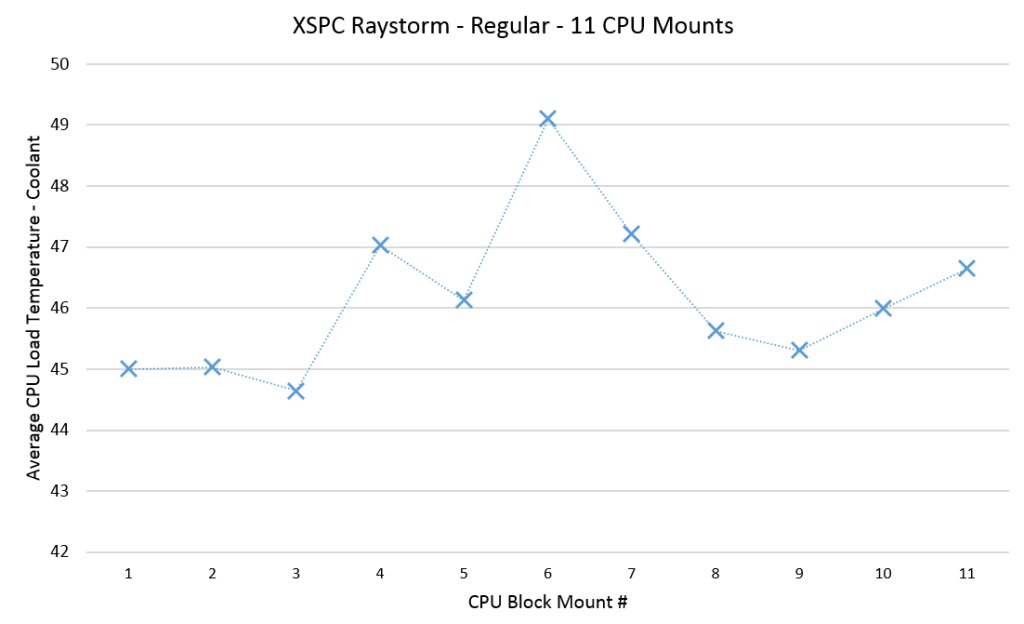
As I was working on the 5820K based CPU block testing, I had initially decided to run 6 mounts.  However I also wanted to determine how many mounts are enough for the accuracy we want.  After completing 6 mounts on the raystorm there was one particular data point that was far worse than the rest.  In fact it was 5C worse than the best mount.  Typically I would think think this was a setup issue, or I might see an issue with the TIM spread after removing the block.  However everything looked good.  So it’s possible that it simply is legitimate data that shows that a bad mount is possible.  Bear in mind too that I’ve done many hundreds of CPU block mounts – so the likelihood of a bad mount due to “user error” is also low.

Bad mounts seem to be far more likely in my experience when the springs used in the mount are not very “strong” (low K factor).  This means they are less likely to balance the the mounting pressure and therefore more likely to have the block lean to one side.  There also seems to be some correlation of this behaviour with the “worst” orientation of the CPU block.  I.E. When the bow doesn’t match, it’s likely that the block will not align well either.  The raystorm in it’s regular orientation had both of these issues.  In the end I ran 11 mounts to get some confidence in the data and how many mounts were needed to give a good averaged result:

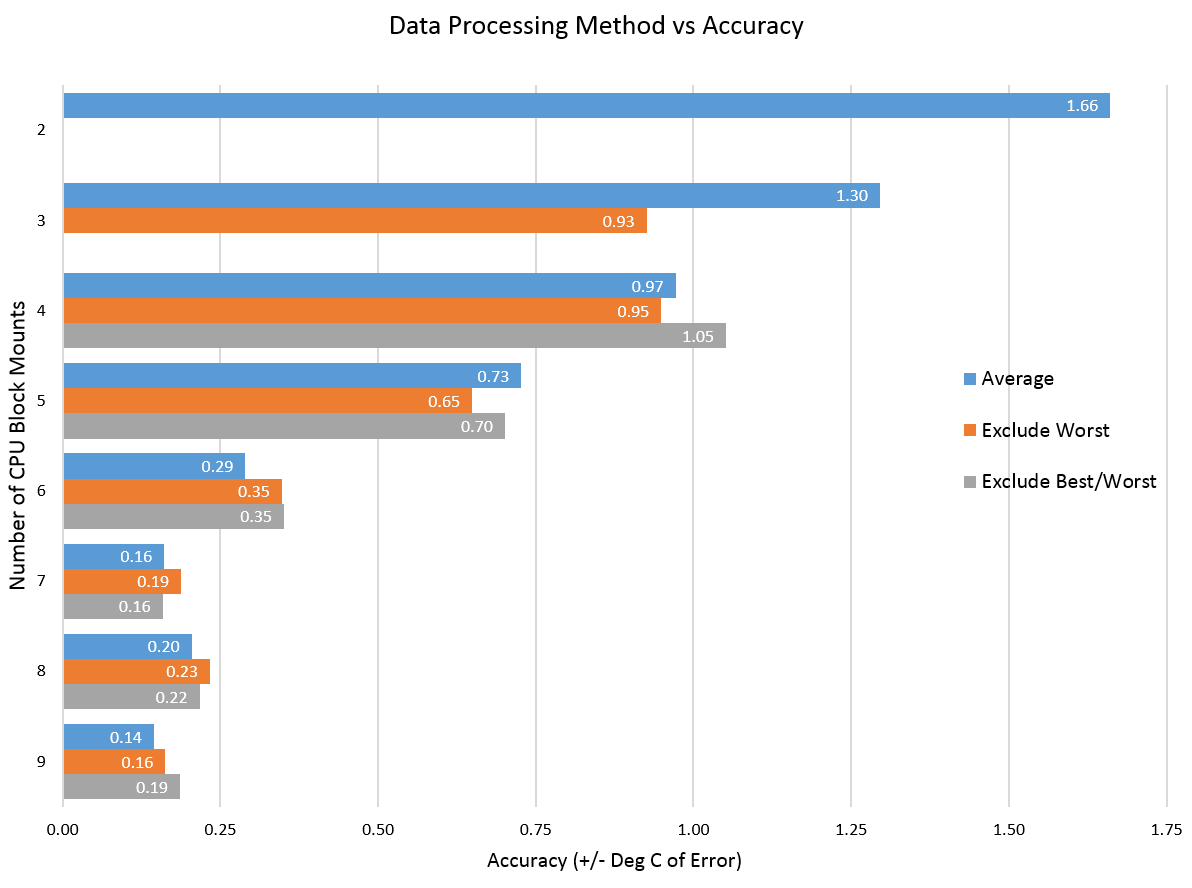
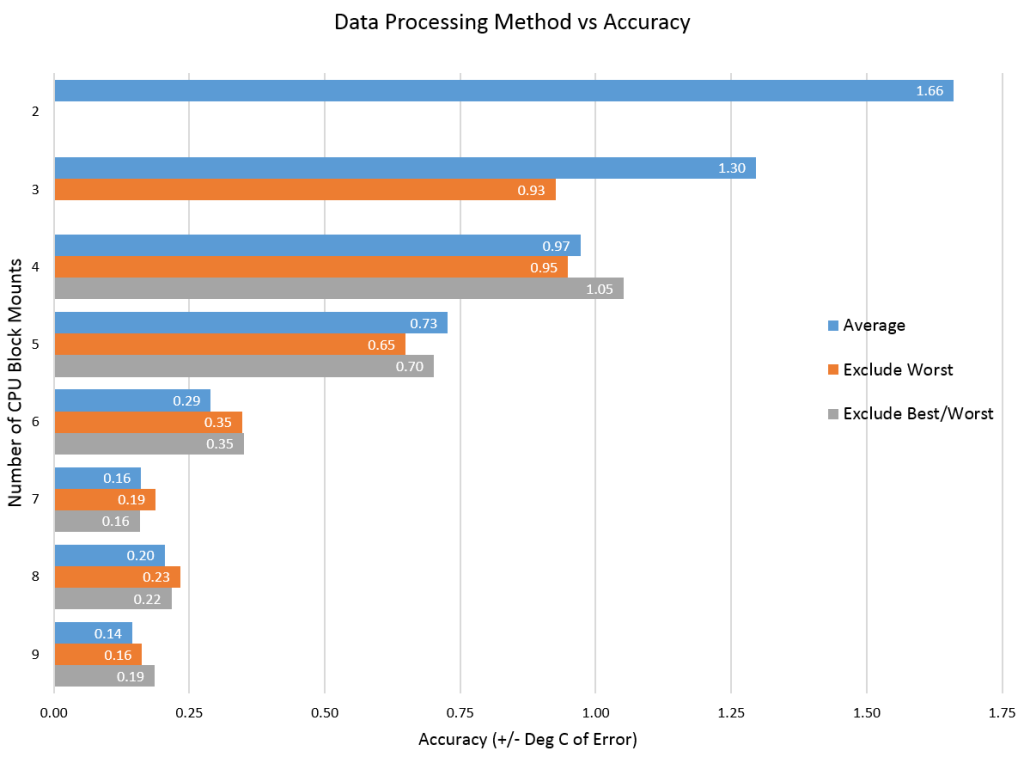
Most blocks only vary about 1-1.5C over the mounts.  So this was some spectacularly bad data.  Let’s take a look at processing it with various methods to see what kind of accuracy we get:

So in order to have < +/- 0.5C of error on this kind of dataset than we need to have at least 6 mounts of the CPU block.  Once you hit 7, any additional runs do not really seem to change the accuracy much – however so much of this is dependent on the luck of the draw – our worst data point was in the middle of the dataset. This means that part of the reason the 6 mount average does well is because that bad data point is then included in every average of 6.  Whether that single data point shows up or not drastically effects the results.  That’s where luck and statistics comes in.  A block might get lucky and have 6 good mounts or 6 bad mounts.  Think of tossing a coin, while unlikely, it is possible for a coin with a 50% possibility of heads or tails to land on heads 6 times in a row.

So increasing the number of runs is also about increasing the number of chances of good/bad mounts as much as it is about increasing the accuracy of the end result.  So if we look at the statistics of data sampling we could say that for an accuracy of 0.5C/5C i.e. 10% we would really need about 100 runs.  This simply is not practical.

Having said that this one data point is messing all the results up, the “exclude” worst methodology doesn’t significantly increase accuracy either.  I’m always reluctant to throw out data without a reason – and showing that excluding the data point doesn’t help much makes me feel better about this principle.

So in summary – what does all this mean?  Clearly the raystorm data here is really pretty bad but it’s also data for the non-optimal mount which we care less about.  Presumably the other tighter data sets will be more accurate – assuming they are representative of the “real data”.  However one thing is clear for poor mounts- even 5/6 mounts may not be enough to get good accurate data and avoid “luck”.For now though given the constraints of time we will continue to run 6 mounts and live with the resulting accuracy.  If we have time we will double back and run more mounts and see if data changes significantly.  For manufacturers though this should be a wake up call that designing a reliable repeatable mount may be more important than they thought given the time limitations that reviewers have.